Ferocious Doves

Last week, we asked ourselves how many smaller equilateral triangles are needed, at a minimum, to cover an equilateral triangle. These smaller triangles don't have to be equal and can overlap. The answer is 3, and we arrive at it by excluding the smallest possibility: it's obviously possible with 3, and it's not difficult to show (how?) that it isn't possible with 2.

Regarding the problem of the 5 points of an equilateral triangle, various approaches have been proposed; the most "pigeonhole" is that of Francisco Montesinos:

“By joining the midpoints of the sides of the original equilateral triangle, we obtain 4 equilateral triangles with sides 1/2 m. Two of the 5 given points will necessarily be within the same triangle of the reduced ones, so their distance d cannot be d>1/2.”

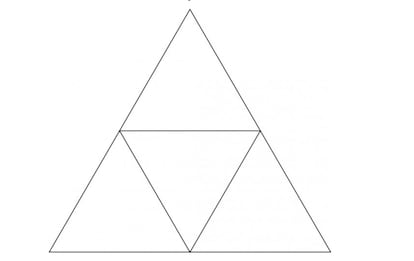
Indeed, by dividing the initial triangle into 4 equal triangles, a pigeon loft with 4 spaces is created, each of which must accommodate 5 pigeons, or points. And the greatest distance that can exist in an equilateral triangle with a side length of 1/2 m is precisely the length of the side, so any two points located within it can, at most, be 1/2 m apart (and are, obviously, the triangle's vertices).

The solution provided by Rafael Granero is somewhat more complicated , but no less interesting:

“Certainly, there are four points that must be the furthest away, and it could even be said that, given four points, they are the furthest they can be from each other: the three vertices and the center. The center is 57.7 cm from any of the three vertices. Any movement, however small, of the point located at the center will inevitably decrease the distance to one or two of the vertices. And the same holds true for each of the points located at the vertices with respect to the other three points. The only points that are more than 50 cm from the center point are those outside a circle of radius 50, centered at the center of the equilateral triangle. But in each of the three zones, all the points are less than 8 cm from the furthest point, which is the vertex, so there is no way to locate a fifth point that is more than 50 cm from the other four.”

As if in passing, the question of how unlikely it is to have to roll a dice 13 times to get 3 equal numbers was asked, and this is Juan Zubieta's answer:

“The probability of reaching roll 13 is the quotient of the possible permutations with 6 pairs of numbers (12!/2^6) and all the possible sequences of rolls (6^12). The result is: 1925/559872 (approximately one chance in 291).” (Remember, it’s not about getting a specific number, such as 6, 3 times, but rather about some number coming up at least 3 times.)

High-risk dovecote

After the training of the last few weeks, and especially dedicated to those who think that the pigeonhole principle is a truism only applicable to the simplest problems , here is a classic that deserved the attention of Paul Erdös himself:

Given the set {1, 2, …, 2n}, show that in any subset of n+1 numbers there will be at least two such that one is a multiple of the other.

Don't try to solve it during the hottest hours: the pigeons in this high-risk loft could fry your brain cells.