Elastiekjes, veren en andere elastische materialen

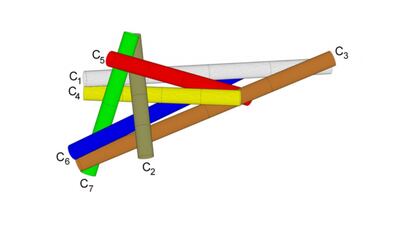
De 6 sigaretten van oneindige lengte van vorige week , die met elkaar in contact kunnen worden gebracht zodat ze elkaar raken, zijn voor verbetering vatbaar: in de afbeelding zien we een oplossing met 7 sigaretten, die bovendien niet uniek is (kunt u er nog één vinden?). Sommige contacten zijn duidelijk, maar andere niet zozeer; Hoe weten we bijvoorbeeld zeker dat de C5-sigaret de C6 raakt?

Wat de vraag over het elastiekje betreft, was dit een strikvraag : als het elastiekje niet in volume veranderde (of, met andere woorden, in dichtheid), zou het oppervlak vier keer kleiner zijn als de diameter van zijn doorsnede werd gehalveerd. De lengte zou dus vier keer groter moeten zijn: 4 meter. Maar als het rubber niet in volume zou afnemen wanneer het wordt uitgerekt, zou het niet elastisch zijn. Het zou lijken op kauwgom en het zou niet zijn oorspronkelijke vorm aannemen wanneer het wordt losgelaten (en dus zou de Poisson-verhouding niet bestaan). Wanneer een elastiekje wordt uitgerekt, rekken de polymeren (zeer lange moleculen) waaruit het bestaat, die in een zigzagpatroon verstrengeld zijn, uit, waardoor het volume afneemt. Wanneer het rubber wordt losgelaten, keren de polymeren terug naar hun oorspronkelijke vorm vanwege de structurele krachten van de lange moleculen. Het is eigenlijk alsof het elastiekje bestaat uit een oneindig aantal microscopisch kleine (of liever gezegd: microfysische) veren, evenveel als er moleculen zijn.

Een veerkrachtig bord

En als we het toch over elasticiteit hebben, ons Carrolliaanse bord van een paar weken geleden was misschien niet zo gek als het in eerste instantie leek. Het bord gebruikte gewoon een aantal concepten op een ietwat elastische manier. Zo kan de gelijkheid 180 = 90 + 30 gewoon onvolledig zijn, en ontbreekt + 60 om de relatie tussen de hoeken van een rechthoekige driehoek, die de helft is van een gelijkzijdige driehoek, compleet te maken.

Daarentegen bedragen de hoeken van een driehoek alleen in het Euclidische vlak 180º. Op het aardoppervlak kan eenvoudig een driehoek worden vastgesteld met hoeken die samen 270º bedragen: het ene hoekpunt kan de Noordpool (of de Zuidpool) zijn en de andere twee kunnen respectievelijk de steden Quito (Ecuador) en Libreville (Gabon) zijn, die beide op de geografische evenaar liggen en ongeveer 10.000 km van elkaar verwijderd zijn.

Wat betreft de rechthoekige driehoek die gedeeltelijk verborgen is door het hoofd van de jonge blondine, als we de 180 daarin negeren, kunnen we denken dat de verborgen waarde van de rechte hoek 70º is; behalve dat het geen sexagesimale graden zijn: de jonge vrouwen in de afbeelding verdelen de omtrek in 280 bogen in plaats van de gebruikelijke 360.

En, zoals Benedicto Torres opmerkt, kan Poisson cursief worden weergegeven omdat de spellingscontrole het als een vreemd woord beschouwt. Het betekent immers 'vis' in het Frans.

Tot slot, en in lijn met de relatie tussen elastiekjes en veren, een voorstel van onze vaste commentator Francisco Montesinos:

Het volgende gekookte gerecht schiet me te binnen. Laten we aannemen dat een veer met een hoogte van lyn en windingen zo zijn gewikkeld dat ze een cilindrische helix of spiraal met straal r vormen. Vervolgens rekken we het aan één kant uit, terwijl we het andere uiteinde stilhouden, totdat de hoogte verdubbeld is. De vraag is: wat zal de straal van de nieuwe cilindrische spiraal zijn, ervan uitgaande dat de vervorming gelijkmatig is?

Ook: Hoe lang is de afgerolde veer?